You probably think that gyros are well understood, so you may be surprised by what follows.
Newton told us that internally generated forces cannot move the center of mass of a body – you can’t pick yourself up by your own boot laces.
Yet every book ever written about gyroscopes says that the gyro does exactly that! Their authors say that the gyro generates a torque that causes the gyro to precess and, a second torque that holds the gyro up when it precesses steadily. For example, on page 135 of the book “Gyrodynamics and its Engineering Applications” by Arnold and Maunder, there is a drawing which shows the three turning moments that present-day gyro theory says are acting on the gyro. Copyright law prevents me from showing you this picture, but the book is still available, so if you chose to buy it… W is the weight of the gyro and generates a turning force around the horizontal axis through O, which of course tends to make the gyro fall. This is countered, in the theory, by the two turning moments M1 and M2. M1 is centrifugal force, and M2 is the gyro generated torque. I’m going to show you that none of these three turning moments actually exists! Fig 2 shows an idealised version of the toy gyro on an Eiffel Tower that you may have played with as a child. This is the gyroscope configuration we are talking about. It’s often referred to as an offset gyro.
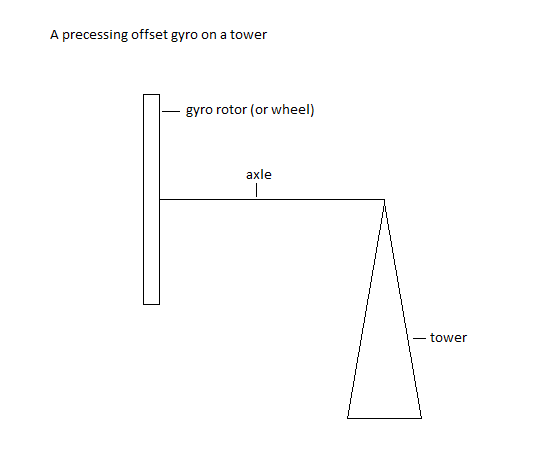
Fig 2
The gyro certainly does generate torques, and the best book I ever read that deals with these in a clear, quantitative way, is “Meaningful Engineering Science” by S. H. Rutherford, (Mechanical Engineering Publications 1980).
Rutherford’s analysis makes it absolutely clear that the forces generated by the gyro are just centrifugal force due to the fact that the particles making up the gyro wheel are following curved paths, as shown on page 9 of Rutherford’s book. The gyro generated torque is therefore internally generated and, as Newton said, cannot move the center of mass of the gyro.
So, if its not the torques, what does cause the gyro to precess, and what does hold it up? We can show mathematically that when an offset gyro is spun up and released, it loses mass. Fig 4 is such a gyro.
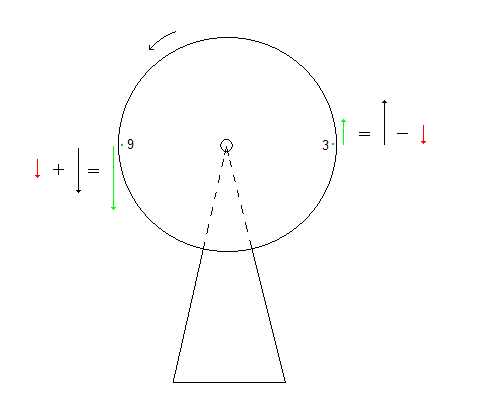
Fig 4
It is immediately obvious that the particles in the gyro rim at 3 o’clock and 9 o’clock are subject to different effects on their mass. They travel at different absolute velocities and experience different effects due to the gravitational field.
The red arrows are the velocity vectors due to the whole gyro wheel falling, the black arrows are the velocity vectors of the particles due to the spin of the wheel . The green arrows are the vector sum of these. Clearly the velocity and thus the mass of the particle at 3 o’clock is less than the particle at 9 o’clock. The Visual Basic code that quantifies these effects (see fig 5) is provided on the Gravity page. The bottom line is that the gyro loses mass as it falls.
Fig 5
Of course, Nature will not allow this. The gyro accelerates sideways (begins to precess) in order to compensate for these mass losses and thus conserve energy.
The idea of a particle accelerating spontaneously isn’t quite heresy. Modern physics books tell us that a stationary free neutron decays after about 15 minutes into a proton and an electron (a neutrino is also produced). The total rest mass of the decay products is less than the rest mass of the neutron, so the particles fly away at very high speed in order to increase their mass. There is no explosion, no flash of light, the proton and electron just hit the ground running.
And so the falling wheel of the gyro in Fig 4 spontaneously starts to move sideways to keep its mass constant and preserve the law of conservation of energy.
Clearly, the sideways component of its motion doesn’t take it into stronger gravity, so its ADG reduces as it falls. At the bottom of the cusp (Fig 5) it isn’t trying to fall at all, its just moving sideways. Its ADG is zero. It’s worth repeating; the model shows mathematically that as the gyro falls, its ADG reduces, so it tends to fall less quickly, and so its mass tends to reduce. Nature won’t let this happen, so the gyro accelerates sideways. This is additional to the acceleration due to the mass loss shown in Fig 4.
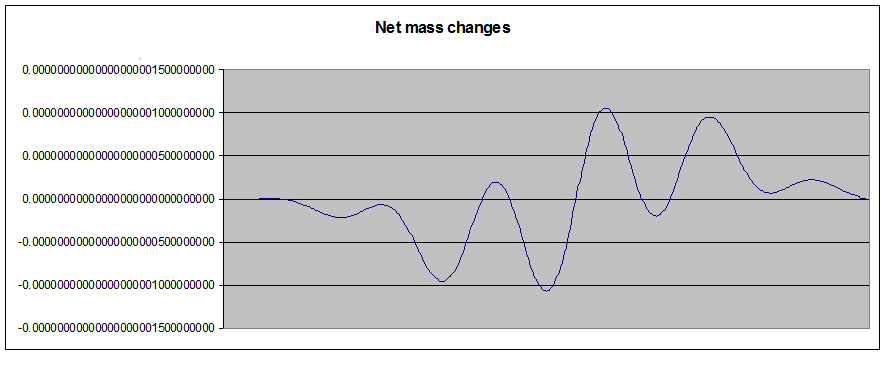
Fig 6
Fig 6 shows the net mass changes for two particles of arbitrary mass at 9 and 3 o’clock over one nutation cycle.
We’ve shown on the Gravity page how a gyro becomes weightless – its ADG falls to zero – as it falls and precesses, but there is another way to show that the gyro wheel is weightless. We can make better progress if, instead of thinking about weight, we think about acceleration due to gravity (usually shortened to ‘g’ but I prefer ADG to avoid ambiguity). Close to the surface of the Earth the acceleration due to gravity (ADG) is approximately 9.8 m/s/s. On the Moon it is about 1.6 m/s/s. On a small asteroid it would be a tiny fraction of that. If the acceleration due to gravity of a body in the earth’s gravitational field were to reduce to zero it would be floating in the gravitational field – i.e. it would be gravitationally buoyant. So, if a body has no weight it is gravitationally buoyant – its ADG is zero. Fig 7 shows the turning moment produced by the gyro.

Fig 7
Fig 8 shows ALL the turning moments about the horizontal axis through the center of mass (COM) of the gyro. These are the gyro generated torque IΩω and the reaction force Mg from the top of the tower acting through R its distance from that axis.
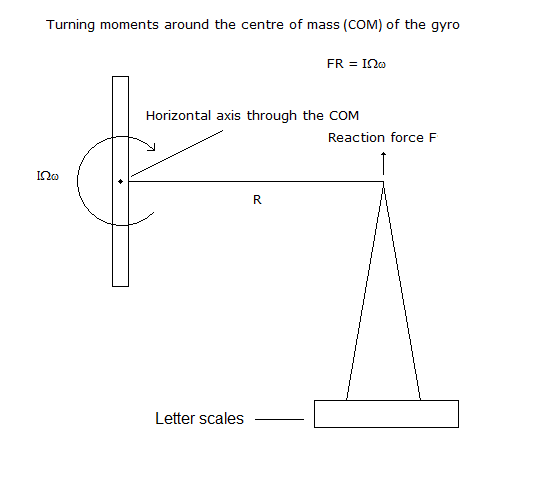
Fig 8
Fig 8 shows the offset gyro standing on a set of scales so that it can be weighed. What will the scales register? I assure you they show the same reading as they do when the gyro is not precessing and all the gyro parts are piled on the scales.
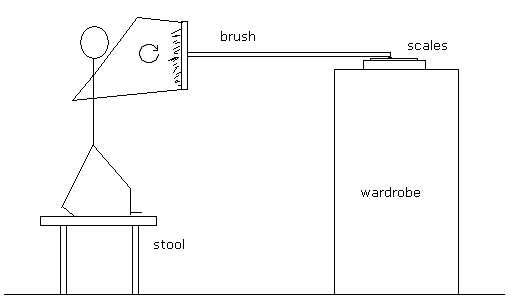
Fig 9
If we looked at the scales on top of the wardrobe in Fig 9 we would see that the stick man is able to register a reading. In the same way that the gyro does, though he can’t transfer all his weight to the wardrobe scales. The best he can do is distribute his weight between the two sets of scales. Of course he doesn’t have a mechanism to reduce his ADG to zero like the gyro does. So if the gyro generated torque IΩω, presses down on the top of the tower, the scales must register that downward force just as they do for the stick man. The gyros weight can’t also press down on the tower or the scales would register a reading greater than its weight. It doesn’t; Nature is clever enough to make the force due to the gyro generated torque equal to its weight. It isn’t the first time Nature has fooled us this way.
