The force of gravity
Einstein showed that there is no force of gravity holding the Moon in orbit around the Earth and no force of gravity keeping them both orbiting the Sun.
Newton developed a very successful theory of gravity, but Einstein showed that it was wrong. In Newton’s theory, a “force of gravity” existed between any two massive bodies M1 and m2 such as the Earth and the Moon. The magnitude of the force he said was Fg = G M1 m2 / R2 where G is a universal constant and R the distance between the centres of mass of the bodies.
All unpowered bodies moving in the gravitational fields of bodies such as the Earth and the Moon are in freefall and follow trajectories that are determined by the law of conservation of energy.
Despite this, when NASA sent the Cassini probe through the rings of Saturn, scientists used Newtons laws to calculate its course and trajectory. It would have been impossible to calculate using Einstein’s equations.
The only time nature produces an actual “force of gravity” is when a particle in a gravitational field is constrained, i.e. is prevented from falling freely towards the centre of mass of the body producing the field.
We now describe how that force arises. We imagine throwing two identical particles (carbon atoms for example), A and C (at the bottom right of the freefall matrix below, fig 1), vertically upwards with slightly different energies. The A particle thus rises to a slightly greater height (B) than the C particle (which rises to D). At the exact moment that A stops rising we imagine sliding a rigid shelf under the particle. It continues to fall the very small distance from B to D until the mutual repulsion of its negatively charged outer electrons and the negatively charged electrons in the atoms of the shelf, bring it to rest. As it falls from B to D, nature applies an increasing downward force. This is the actual force of gravity.
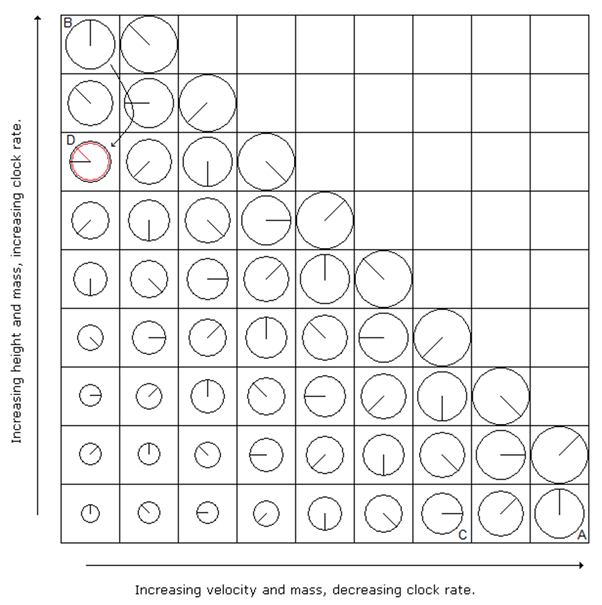
Fig 1
The product of the average value of this force and the distance B to D is called the particle’s gravitational self energy. It is stored as a deformation of the electric fields of the particle and the atoms of the shelf. Thus when the particle comes to rest, it has less mass (shown in red) than an identical particle (shown in black) at the same height but in free fall. We say the red particle is “off matrix” and corollary 1 of the Mass Clock-rate Principle (MCP) says that it must therefore be subject to a downward force – the force of gravity.
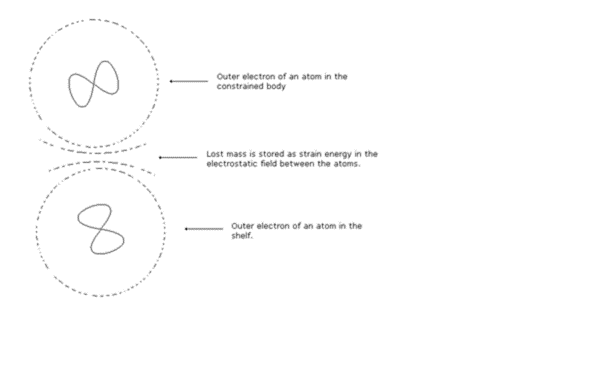
Fig 2
Gravitational Self Energy
When a body is constrained, it loses an amount of energy as it “settles” which we call Gravitational Self Energy. Numerically, it is the energy that would be stored in a helical spring attached to the top of the body and which is then used to just lift the body off the ground. The origin of this energy is explained in the section above, “The force of gravity”.
Free fall
There are two quite different forms of free fall. Einstein explained that in orbital free fall a body is following a “straight line” path in curved space. But when we drop something and it falls radially towards the centre of the earth, a completely different mechanism is at work.
Theory of Radial Free fall
To understand why bodies fall radially in a gravitational field we need to consider two well proven facts from relativity theory. First, Special Relativity tells us that if a body’s velocity increases, its mass also increases. Second, in General Relativity Einstein tells us that no force acts on a body in free fall (whether orbital or radial). The mass of the body must therefore remain constant as it falls. This means that if it gains mass as it accelerates, then it must also lose mass by some means. It is the effect of the gravitational field on the wavelength of the particles making up a body that causes it to lose mass. By increasing their wavelength, the gravitational field reduces their energy and therefore their mass.
As they accelerate downward to compensate for this they enter stronger gravity and lose more mass and must accelerate again to conserve energy. Close to the surface of the Earth an acceleration of approximately 9.8 m/s/s accomplishes this.
Logically the mass loss due to gravity must occur before there can be a mass gain due to velocity. The uncertainty principle allows the momentary violation of energy conservation that this requires and sets a limit on the delay between mass loss and mass gain. Certainly, in order to make any progress with understanding the phenomenon it is necessary to treat this as a two-step process, and accept that the second step, an increase in velocity, cannot happen without the first step – a loss of mass due to the particle’s interaction with the gravitational field, for if there were no mass loss, the body would not fall.
It is helpful to quantify these steps.
In the drawing below (fig 3), a 1kg body in free fall accelerates at 10 m/s/s for three seconds starting at zero velocity (and, for convenience, 1000 metres above the surface of the earth). Because this is only for illustration, the fact that g increases as the body falls, is ignored. We should really recalculate g continuously by dividing the Standard Gravitational Parameter (μ) by the square of the distance of the body from the centre of the earth.

Fig 3
The drawing shows the distances fallen each second and the velocity reached.
It also shows the actual mass at the end of each second calculated using the Lorentz transformation equation m1 = m0 / Sqrt (1 – v2/c2).
The mass increase from one second to the next is also shown. Note: it’s the increase in velocity that produces the increase in mass.
For simplicity we imagine all the mass loss due to gravity occurring at the start of the time period (if we progressively reduce the time period, then in the limit, as ∆t approaches zero, the mass loss and mass gain occur almost simultaneously, which is of course what happens in reality).
So at the start of the first second gravity removes 0.0000000000000005563250280268 kg of mass from the body. By the end of the first second the body has reached a velocity of 10 m/s and gained the same amount of mass.
At the start of the next second, gravity removes 0.0000000000000016689750840804 kg of mass from the body (a greater amount than at the start of the previous second because gravity is stronger 5 metres closer to the earth, and this of course is why the body needs to keep accelerating) and by the end of that second the body has to reach a velocity of 20 m/s and thus gain exactly 0.0000000000000016689750840804 kg of mass in order to conserve mass/energy.
This repeats in the 3rd second and the mass of the body remains constant at 1kg.
Gravitational buoyancy
Close to the surface of the Earth the acceleration due to gravity (ADG) is approximately 9.8 m/s/s. On the Moon it is about 1.6 m/s/s. On a small asteroid it would be a tiny fraction of that. If the acceleration due to gravity of a body in the earth’s gravitational field were to reduce to zero it would be floating in the gravitational field – i.e. it would be gravitationally buoyant.
The acceleration described above, which occurs in order to replace the mass removed by the gravitational field, is directed downwards, but that is not essential; as long as it accelerates it doesn’t matter about the direction. If the body is a spinning offset gyroscope, the gyroscope’s precession acceleration in the horizontal direction contributes to the total acceleration. The actual (downward) acceleration due to gravity plus the (horizontal) precession acceleration make up the total acceleration needed to conserve mass/energy.
However, the horizontal component of acceleration does not take the gyro into stronger gravity.
Because the downward component is less than it would be for any other body in free fall, the gyro does not fall as far, does not have its mass reduced as much and thus requires a reduced downward acceleration. As the attached mathematical model (fig 5) shows, the downward acceleration reduces continuously as the gyro generated horizontal acceleration increases. As shown below (fig 4), at the bottom of the nutation cusp, the acceleration due to gravity (shown as A_ADG) approaches zero – the gyro no longer exhibits any tendency to fall. It is gravitationally buoyant – it is weightless!
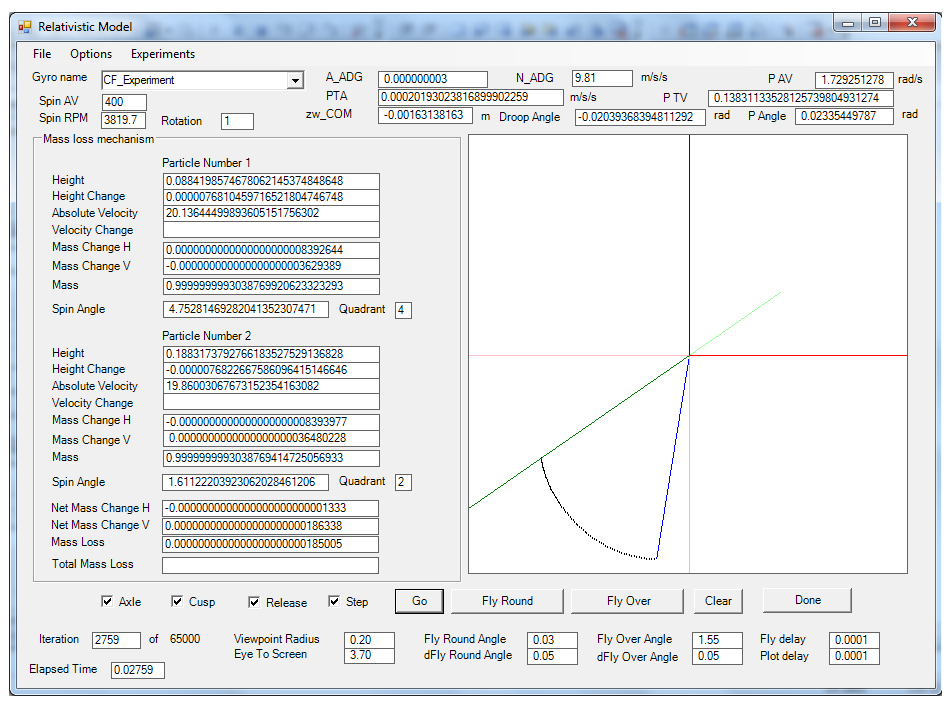
Fig 4

Fig 5
