Papers – gyrodynamics

This page contains a number of my scientific papers, none of which has been published.

The Mass, Clock rate Principle

In 1923, when de Broglie suggested that the electron had an internal clock and that time dilation effects were entirely internal to the particle, the success of special and general relativity ensured that he was ignored.

However, in 2008, a French team showed that the electron does indeed have an internal clock (see “Reading the Electron Clock” David Hestenes, arXiv:0802.3227v1, 21 Feb 2008).

Here we discuss some changes to relativity that are required in order to take account of the fact that the electron has a clock.

When a material particle or a body, which could for convenience be an atomic clock, rises at constant (slow) speed in a gravitational field, both its mass and its clock rate increase. When a particle or body accelerates, its mass increases, but its clock rate reduces.

If it were not for this asymmetry, there would be no way to distinguish between a change in mass caused by acceleration and a change in mass caused by gravity.

Nature needs to be able to make this distinction because if a body is accelerated to a given speed and then the force is removed, Nature also removes the inertia force, but if a body is lifted to a given height, the lifting force must be maintained or the body would fall again, so Nature has to apply an opposing force – the body’s weight.

The Mass Clock-rate Principle asserts that…

All adjacent, co-moving, like particles have the same mass and clock rate, regardless of their state of motion or position in a gravitational field.

The Mass Clock rate Principle (MCP), is clearly true. No heavy, or light, material particles (fermions) are found in Nature. For example, all the single outer emission electrons of every atom in any sample of cesium 133 have exactly the same mass. If they did not, cesium atomic clocks would not work so well. Such clocks depend on the hyperfine frequencies of the microwave emissions of the cesium atoms and those frequencies depend on the mass of the emitting electron. The relationship between emitted frequency and electron mass is,

o = eH/4pmc

where o is the Larmor Frequency and m is the electron mass; everything else is a constant. The Larmor Frequency is the frequency of precession of the orbiting electron¹.

Also there is universal agreement that material particles possess some kind of internal clock that is affected by acceleration and gravity in the way described by Einstein. Muon decay experiments provide some evidence, but present day theories offer no explanation of the underlying mechanism.

What is proposed here is that Nature “monitors” the mass and clock rate of all particles in order to maintain the MCP, and when exceptions occur, attempts to correct the deviation by, for example, applying a force.

The Relativistic anomaly

The anomaly is best described with reference to the L shaped matrix of test particles shown below (fig 1).

During acceleration (the lowest horizontal row) a particle gains mass (depicted by the increase in size²), and its clock rate reduces³ (depicted by the anticlockwise movement of the ‘clock hand’). If we raise a particle at constant speed in a gravitational field (the leftmost column), again its mass increases, but in this case its clock rate increases.

The L matrix

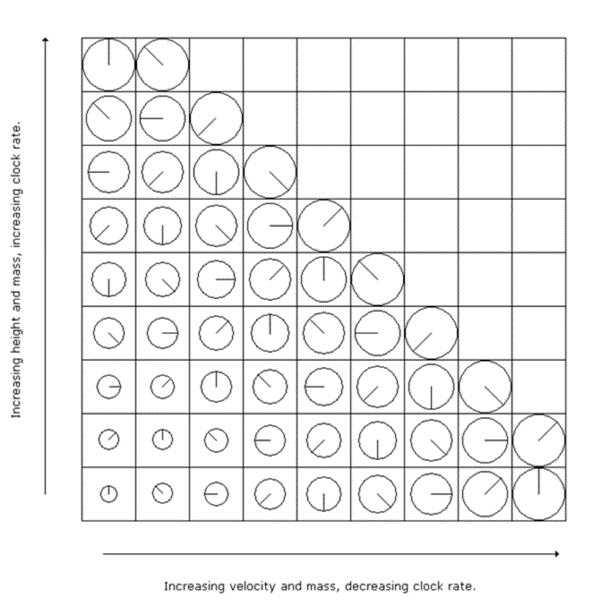
Fig 1

Mathematically the anomaly is accommodated by the different equations we use to calculate clock rate and mass during acceleration and in gravitational fields. During acceleration we use the gamma factor⁴, which increases the length of a second, thus reducing clock rate.

s₁ = s₀ / Sqrt (1 – v²/c²)

The same form of equation is used to calculate the increase in mass during acceleration.

m₁ = m₀ / Sqrt (1 – v²/c²)

The equation we use to calculate the clock rate and mass of a particle as it rises at constant speed in a gravitational field is the redshift equation⁵, which increases the characteristic frequency of the light emitted by atoms, and thus increases clock rate.

f₁ = f₀ * (1 – (GM / R c²))

Again, the same form of equation is used to calculate the increase in mass.

m₁ = m₀ * (1 – (GM / R c²))

We have to talk about the light emitted by atoms because individual particles don’t emit any characteristic (i.e. discrete) frequencies. However, relativity theory makes no distinction between atoms and the individual particles they contain. Time dilation applies to the electron and the proton as well as to the hydrogen atom they may form. Furthermore, De Broglie showed that all particles have a frequency f = E/h (where E is the total energy of the particle and h is Plank’s constant). The best known experimental evidence that individual particles have a clock rate are the 1977 CERN experiments which showed that muon decay – a statistical effect – agrees with Einstein’s time dilation prediction to within one part in 500.

How Nature maintains The Mass Clock rate Principle

The following examples show that Nature’s main strategy is to apply a force when exceptions occur. A freely falling body experiences no force of gravity, but the moment it is constrained, the gravitational force is applied. For example, a cricket ball falling radially towards the Earth, experiences no force of gravity. Only when we begin to constrain the ball by catching it, does the force of gravity “pop out” of empty space to do work on the ball (and our hand).

A body moving at constant speed in free space is also free from forces, but if an external force is applied, the inertia force⁶ is instantly in evidence, controlling the change in mass and clock rate of the particles of the body.

Nature has a second strategy for maintaining the mass clock rate principle. This is manifest in neutron decay⁷. If a neutron is displaced from an atomic nucleus, it is unstable, with a half-life of about 15 minutes. When the neutron decays, it transmutes into a proton, an electron and an electron anti-neutrino. Here, two oppositely charged particles – the proton and the electron, which would ordinarily attract each other strongly, fly apart at great speed. There is no period of acceleration and no force driving their exit from the decay site; the particles are created travelling at high speeds, in clear violation of the law of inertia.

Obviously Nature does not need a force or a period of acceleration if the mass and clock rate are already set appropriately, and furthermore, seems able to switch off the electrostatic attraction between electron and proton, or work would have to be done against this attractive force; and no source of energy is available.

Consequently, just as velocity and position in a gravitational field completely determine a particle’s mass and clock rate, the facts of neutron decay force us to conclude that the converse is also true: – mass and clock rate completely determine the velocity of a particle or body.

The problem of moving a body radially in a gravitational field or linearly in free space therefore reduces to the problem of changing the mass and clock rate of the particles of the body we are trying to move. The reader is reminded how easily we can change these values simultaneously through appropriate accelerations or change of position in the gravitational field. The real problem is changing mass and clock rate independently. That Nature allows this is clearly shown by the anomaly that prompted this investigation.

Unconstrained (free fall) particles

The matrix below (fig 2), depicts a vertical slice through spacetime close to the surface of a massive body such as the Earth. The pairs of values are placeholders for the actual values of mass and clock rate of a particle at that height, in free fall, and momentarily at rest with respect to the Earth⁸. In the drawing, mass and clock rate are set arbitrarily to 10 near to the surface of the planet, increasing continuously with increasing height. Mass and clock rate values are made the same for convenience.

The right-hand half of the matrix shows the velocity domain. The velocities shown below the matrix again are arbitrary and serve merely to indicate increasing velocity. The left-hand element of each pair of values represents mass, the right-hand element represents clock rate. The rows of cells in the gravity domain represent shells of identical mass and clock rate values for particles stationary with respect to the Earth. The cells in the acceleration domain represent the unique pairs of values of mass and clock rate for a particle at that height and travelling at that speed.

Matrix 1

Fig 2

What is Free Fall?

We imagine a single particle alone in space, and assert that it has its maximum possible mass. We need to add the proviso that the particle is stationary, and we can only reasonably do that by saying that it is stationary relative to an absolute space – the absolute space behind the problem of “Newton’s bucket” ¹⁰. Introducing this particle into the real universe will immediately reduce that mass due to the effect of gravitational fields. Nature instantly accelerates the particle in order to make up the lost mass. Thus the particle retains its “empty space” mass value, but at the cost of being in motion towards the local source of gravity. This motion leads it into stronger gravity, which further reduces its mass, and Nature responds by making it go faster, thus increasing its mass. There can be no force involved in this continuous process or the particle would gain mass, and we know its mass stays constant. If no force accelerates the particle, it is convenient to describe the particle as having a “tendency” to accelerate. Force, tendency and instant change in velocity are all strategies Nature applies in order to maintain the Mass Clock-rate Principle.

Gravitational Binding Energy

Everything discussed so far relates to particles in free fall. Before we consider constrained particles and the gravitational force, it will be helpful to review the conventional concept of Gravitational Binding Energy, which is usually described in Newtonian terms as being the negative of gravitational potential energy – the energy needed to raise a body to “infinity”.

In relativistic terms it is the mass lost by a material particle brought to earth at constant speed from infinity.

Taking a common sense approach to the concept of “infinity”, we should think of gravitational binding energy as the difference in mass between a particle on the surface of the earth and a similar particle in “free space” between the galaxies.

Hence, a particle close to the surface of the Earth, projected upwards, and at the top of its trajectory, has a mass value as determined by the L matrix, which is the difference between its free space value and its gravitational binding energy.

Constrained particles and Gravitational Self Energy

In addition to the above concept of gravitational binding energy, constrained bodies, i.e. anything not in free fall, including you and me and everything in and on the Earth, are subject to a reduction in mass of about 1 billionth of their free fall mass, which is conventionally referred to as “Gravitational Self Energy” – GSE, (or confusingly just Gravitational Binding Energy.) A better name might be, “Latent Gravitational Binding Energy” – LGBE, since it is the mass we have to add to a body in order to just lift it off the surface of the earth.

A constrained particle experiences a downward force – the force of gravity, while all around it, other particles in free fall experience no force at all. The absence of a force on a body in free fall was one of Einstein’s greatest insights. With no force acting, he realised that there can be no change in mass, so that as a body falls, the increase in mass due to its increased velocity must be exactly cancelled by the reduction in mass caused by stronger gravity as its height in the field reduces. That Einstein’s conjecture was correct, was proved experimentally by Eric Rogers⁹.

Gravitational Self Energy

We will now show how LGBE (or Gravitational Self Energy) comes about. If we slide a rigid “shelf” under an upwardly projected particle at the top of its trajectory, the particle continues to fall for a very short distance. It thus loses mass which it cannot regain by accelerating as it would in free fall. Also its clock rate reduces due to the stronger gravity it encounters as it continues to fall, but only half as much as it would in free fall, when acceleration would further reduce its clock rate.

It is best to think of twin particles projected (thrown) upwards with the same energy. At the top of their trajectories, one is constrained, the other allowed to fall freely. The constrained particle will continue to fall a short distance losing mass due to the stronger gravity it encounters. Its clock rate will reduce for the same reason, but as stated above will not be further reduced by increased velocity.

Therefore, as the free fall twin passes the level at which the constrained twin will come to rest, its mass will be greater and its clock rate slower than the constrained particle. The constrained particle therefore violates the mass clock rate principle and is subject to a force (it’s weight), which is Nature’s attempt to set it falling freely again. The drawing below (fig 3), depicts the outer orbital electron of an atom in the surface of a body being constrained by the electrostatic field (the Van der Waals force) of the outer electron of an atom in the surface of the shelf. As the particles begin to interact, the force of gravity “pops out” of space and begins doing work on the particle, forcing it as close as it can to the particle in the shelf. The lost mass is thus converted to strain energy in the intervening electrostatic field. When the constraint is removed, the strain energy (LGBE) is dissipated.

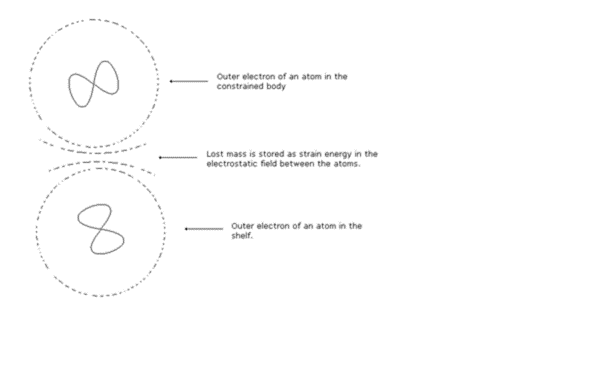
Fig 3

This reduction in mass, analogous to nuclear binding energy, is the energy which binds us to the surface of our planet. Like nuclear binding energy, the process cannot be observed or its value calculated.

The different effects on clock rate in different situations is absolutely crucial to the working of the universe. Imagine that we throw a body upwards and catch it at the top of its trajectory. We know that it will lose a small amount of its mass as gravitational self energy. Now imagine the same body travelling at some speed in free space. We apply a retarding force which reduces its mass by the same amount. In the latter case Nature does nothing, but in the former case she applies the force of gravity to try to get the body back into free fall. If it were not for the completely opposite effects on clock rate, Nature would not know whether to apply the force of gravity or do nothing. The upshot would be that sometimes when we decelerate a body, Nature would apply a force to accelerate it again. Newton’s Laws would not exist and chaos would reign.

It’s important to realise that these changes in mass and clock rate are unimaginably precise, and tied tightly to the position in the gravitational field and absolute velocity of the particle. Nature responds instantly to any violation by changing the position or velocity of the particle (e.g. the instantaneous change in velocity of the electron produced in neutron decay. The electron goes from rest to near light speed in zero time). If the particle is constrained, Nature instantly applies a force to try to restore the mass and clock rate of the particle to their proper L Matrix values.

Sample calculations are shown below. These are verified by comparing the results with their approximate Newtonian equivalents.

Public Sub CalculateLMatrix()

‘ Acceleration Due to Gravity

ADG = 9.8

‘ m0 is the mass in free space, set here at 1.

m0 = 1

‘ m1 is the mass at the surface of the earth. The equation used is…

‘ m1 = m0 * (1 – (G * M / R * c ^ 2)) See reference 5 of the Mass Clock-rate Principle paper – the redshift equation.

m1 = m0 * (1 – ((GravitationalConstant * EarthMass) / (EarthRadius * (SpeedOfLight ^ 2))))

‘ m1 = 0.999999999303607

‘ m2 is the mass at 1000 m above the earth.

r2 = 1000

m2 = m0 * (1 – ((GravitationalConstant * EarthMass) / ((EarthRadius + r2) * (SpeedOfLight ^ 2))))

‘ m2 = 0.999999999303716

‘ mv1 is the mass at 140 m/s . (See reference 4 of the Mass Clock-rate Principle paper – the gamma factor (Lorentz transformation)).

v1 = 140 ‘ m/s

mv1 = m1 * 1 / (Sqr(1 – ((v1 ^ 2) / (SpeedOfLight ^ 2))))

‘ mv1 = 0.999999999303716

‘ Which shows that if a body is accelerated to 140 m/s its mass increases by the same amount that it would if raised at constant velocity to a height of 1000 metres.

‘ As a rough check using Newtonian mechanics…

PE = m2 * ADG * r1 ‘ PE = 9799.99999317642 (PE = gravitational Potential Energy)

KE = 0.5 * mv * v1 ^ 2 ‘ KE = 9799.99999317641 (KE = Kinetic Energy)

End Sub

Notes and references:

“Atomic Spectra and Atomic Structure”, Herzberg, page 103.
Though of course real particles shrink in size as they gain mass since their De Broglie wavelength reduces.
The L Matrix helps us to keep track of the changes in clock rate. If we imagine the particle ‘rolling’ along the axes, a counter-clockwise movement of the ‘hand’ indicates a slowing of clock rate; a clockwise movement indicates an increase in clock rate. Note that the diagonals show the constant mass of a particle during free fall. (Free fall should be taken as including bodies rising freely as when a ball is thrown upwards.)
“Modern Physics”, Tipler and Llewellyn, page 77.
“Modern Physics”, Tipler and Llewellyn, page 110.
A modern view describing inertia as an interaction with the Higgs field can be found in, “The fabric of the cosmos”, Brian Greene, page 261.
For an excellent description see, “The forces of nature”, P C W Davies, page 63.
The mass of a particle in free fall is constant, but if a particle is projected upwards, its clock rate increases as it rises and then decreases as it falls. To obtain a standard value of mass and clock rate for a particle we imagine a particle projected upwards, and take the values of mass and clock rate at the top of its trajectory where it can be considered to be momentarily stationary.
Andrew Robinson, “Einstein. A hundred years of Relativity”, page 225

The Theory of the Inertial Field

Many scientists, including Nordstom, Kaluza, Rosen and Gödel, have at different times and for different reasons, proposed the existence of a universal background scalar field. Gödel called it an “inertial field”. More recently Higgs and others proposed, as part of the standard model, that such a field is responsible for giving material particles their (inertial) mass. It is now called the Higgs Field, and the quantum of the field – the so called Higgs Boson, may have been detected at CERN. However, despite its undoubted success, the Higgs Mechanism is not well defined.

Beginning in 1983, we approached the questions of particle mass and particle inertia by first developing a particle “design” that separates particle charge and particle gravitational mass (see “Fermion Theory”), and treats particle inertia as a separate phenomenon. From 2006 we began to think of inertia as being caused by the interaction of the particle with a background “inertial field”.

Justification

There is a magnetic force and a magnetic field, an electric force and an electric field, a gravitational force and a gravitational field. There is also an inertia force – the resistance you feel when you try to accelerate a loaded shopping trolley – but no inertial field.

Arguments of symmetry suggest that there should be such a field.

Properties of the field

If we assume that the inertial field has the opposite effect to gravity on the speed of light, then our fermion theory explains inertia in a logically consistent way (not described here). (The slowing of light by stronger gravity is equivalent to increasing the length of measuring rods and slowing down clocks. So the inertial field shortens measuring rods and speeds up clocks.)

It also explains the dark matter halos around galaxies… As described by the theory of radial free fall (see Gravity page), a gravitational field increases the de Broglie wavelength of a particle and thus reduces its mass. The inertial field does the opposite. Though the inertial field is a scalar field, its strength effectively increases as the strength of the gravitational field with which it coexists, reduces.

Close to a body like the earth, the effect of the inertial field is much less than the effect of the local gravitational field. But as we move out towards the edges of the galaxy, gravity gets weaker, and at some point, its effects are exactly equal and opposite to the effects of the inertial field. We refer to this as the “transition shell” where gravity still causes a small increase in the wavelength of a particle but the inertial field decreases its wavelength by the same amount.

At the transition shell the mass reducing effect of the galaxy’s gravitational field is exactly cancelled by the mass increasing effect of the inertial field and the particle thus has zero acceleration due to gravity i.e. – it is gravitationally buoyant.

During the quasar stage of the evolution of a galaxy, huge quantities of fermionic matter are thrown radially outwards away from the central black hole. The ADG of the particles thrown out by the quasar of course reduces as they move outwards towards the edges of the galaxy. Were it not for the inertial field, they would always have some finite ADG and would eventually stop rising and fall back into the galaxy (unless they started with the escape velocity for that galaxy). The inertial field changes that: at the transition shell their ADG falls to zero. The particles have become gravitationally buoyant and are no longer attracted back into the galaxy. Galaxies should thus be surrounded by a cloud of matter that is not attracted gravitationally towards the galaxy. The particles in this cloud are attracted gravitationally to each other, but the effect of the inertial field swamps this attraction. Thus, stars will not form from this matter. These “dark matter halos” around galaxies and galaxy clusters have of course been observed and are presently the focus of much attention.

Our work on the theory of the inertial field is ongoing, but we are reasonably sure that the inertial field is responsible for the unusual experimental results we obtained in 2006. We think it is also responsible for the damping of nutation of an offset gyro. The exact mechanisms have not yet been fully worked out, and some of the experiments we propose are aimed at increasing our understanding.

On the Conservation of Angular Momentum

Angular momentum is universally believed to be a fundamental conserved quantity. Experiments have shown that in isolated spinning systems where the distribution of mass is changing, angular momentum is always conserved. Consequently, we never ask how it is conserved, we simply accept it as one of Nature’s laws.

A familiar example is provided by the ice skater who executes a fast spin by pulling her arms inward as she leaps into the air. It is well known however, and shown here for completeness, that though angular momentum is indeed conserved, the rotational kinetic energy of such systems increases in the process. Wherever there is an increase in kinetic energy, we expect to find an unbalanced force at work.

Here we show that the force is centrifugal force. More importantly, we show that the conservation of angular momentum is not a fundamental law that we can never understand, but a subtle, and beautiful mechanism.

We provide a first principles computer mathematical model which conserves angular momentum to twelve significant figures and present the results of an experiment which simulates the spinning skater, along with a computer numerical model of this experiment which also conserves angular momentum and energy.

Centrifugal Force.

There is a widespread belief that centrifugal force is a ‘fictitious force’ – an illusion caused by the moving reference frame of the observer. We must address this misunderstanding before we can proceed to describe the mechanism responsible for the conservation of angular momentum.

We start with what is not in dispute. Fictitious forces are reference frame dependent: there are some well known examples. The pendulum in Foucault’s experiment appears to be pushed by some unknown force when viewed from an earth-bound reference frame. When we view the experiment from space, we see the earth rotating with respect to the ‘fixed stars,’ and the pendulum swinging in a plane which is also fixed with respect to those fixed stars. If the pendulum continues to swing in the same plane but the earth rotates under it, to the earth-bound observer the pendulum will appear to rotate. Thus it was that Foucault proved that the earth was rotating with respect to the fixed stars.

Similarly, a ball placed on the flat top of the dashboard of a car will roll as the driver executes a turn. The driver might interpret this as evidence of a force pushing the ball. Flying above the driver in a helicopter, we see that the ball is continuing in its uniform motion in a straight line as the car moves sideways under it.

In both cases, the observer who is rotating is the victim of an illusion. There is no real force, it is fictitious, and the physical manifestation of that fictitious force (the ‘rotation’ of the pendulum and the ‘sideways motion’ of the ball) switches on and off as we switch between reference frames.

The physical effects of centrifugal force do not switch on and off as we switch reference frames. Consider an engineer on the rotating earth studying the equatorial bulge. He will measure this 21-km radial bulge and judge it to be the result of the centrifugal force experienced by the planet due to its rotation with respect to the fixed stars. At the same moment, an engineer out in space will measure exactly the same bulge and reach the same conclusion as to its origin.

A more dynamic thought experiment serves to show that centrifugal force is real enough to do work. If we attach a rope to the handle of a bucket, half full of water, and whirl the bucket round in a vertical plane, provided it spins fast enough, the water will remain in the bucket. If we replace the rigid bottom of the bucket with a rubber diaphragm, we will see the bottom bulge out. If we spin the bucket faster, the bulge will grow. Since the stretched rubber stores energy, a force must have done work on it.

When the angular velocity of rotation is steady, the rubber diaphragm exerts a centripetal force on the water and the water exerts a balancing centrifugal force on the diaphragm: – the system is in equilibrium. If the rate of rotation is now increased, an observer riding on the bucket would see the rubber bottom bulge out more and more as the rate of rotation increases and centrifugal force temporarily exceeds centripetal force, doing work on the diaphragm. An observer on the ground would measure the same increase in the bulge. The change of reference frame makes no difference.

Centrifugal force arises when a body rotates with respect to the inertial reference frame defined by the ‘fixed stars’ – it is not dependent on the reference frame of the observer.

Newton was in no doubt about the reality of centrifugal force. He begins Book 1 of The Principia with eight ‘Definitions’. These immediately precede his ‘Axioms, or Laws of Motion’. In the scholium to Definition VIII, the final paragraph contains a discussion of relative and absolute (true) motion. He was clearly aware of the absolute frame of reference provided by a rotating system. He says…

“It is indeed a matter of great difficulty to discover, and effectually to distinguish, the true motion of particular bodies from the apparent; because the parts of that immovable space, in which those motions are performed, do by no means come under the observation of our senses. Yet the thing is not altogether desperate; for we have some arguments to guide us, partly from the apparent motions, which are the differences of the true motions; partly from the forces, which are the causes and effects of the true motion. For instance, if two globes, kept at a given distance one from the other by means of a cord that connects them, were revolved about their common centre of gravity, we might, from the tension of the cord, discover the endeavour of the globes to recede from the axis of their motion, and from thence we might compute the quantity of their circular motions.”… “And thus we might find both the quantity and the determination of this circular motion, even in an immense vacuum, where there was nothing external or sensible with which the globes could be compared. But now, if in that space some remote bodies were placed that kept always a given position one to another, as the fixed stars do in our regions, we could not indeed determine from the relative translation of the globes among those bodies, whether the motion did belong to the globes or to the bodies. But if we observed the cord, and found that its tension was that very tension which the motions of the globes required, we might conclude the motion to be in the globes, and the bodies to be at rest;”

Also, in the scholium following Proposition IV. Theorem IV, he provides an elegant definition of, and in fact ‘invents’, centrifugal force.

Energy in angular momentum conservation.

A skater spins on the ice with her arms outstretched, then draws them closer to her body. Her spin rate increases, and angular momentum is conserved. The earth plays no part in this, since friction between the ice and the skate is negligible. She is, for all practical purposes, an isolated system and no external forces are applied.

If her initial moment of inertia is _i (kg m²) and her initial angular velocity is _i (rad/sec), then her angular momentum is … H = _i _i ( kg m²rad sec^-1 or Joule sec)

If _i = 10 and _i = 2, her angular momentum H = 20. If she then pulls in her arms, so that her final moment of inertia _f becomes 8, then, if angular momentum is conserved, her final angular velocity, _f, must change to 2.5 to keep the product equal to 20.

Initially her kinetic energy is…

E_i = ½ * 10 * 2 * 2 = 20 joules (1a)

and after her moment of inertia has reduced to 8 it is…

E_f = ½ * 8 * 2.5 * 2.5 = 25 joules (1b)

and we see that when angular momentum is conserved, energy has to be put into the system.

If the skater were able to reduce her final moment of inertia still further, say to 5 kg m², then her final angular velocity would be 4 rad/sec and her kinetic energy would have doubled to… E_f = ½ * 5 * 4 * 4 = 40 joules

and we note the remarkable fact that whatever the final moment of inertia _f, just enough energy will be supplied by the skater’s muscles to ensure the conservation of angular momentum. The skater is of course completely unaware of her astonishingly accurate transfer of energy.

If we take the view that angular momentum is a fundamental conserved quantity, then the increase in energy might be explained as being a ‘natural consequence’ of that. However, in all systems where kinetic energy is increasing, experience tells us that we should expect to find an unbalanced force at work. The single exception¹ being the force-free interconversion of kinetic energy and rest energy when a body falls freely in a gravitational field.

It is therefore a matter of great interest, and a large part of the motivation for this work, that the skater is able to apply exactly the right force, to input exactly the right amount of energy, to conserve angular momentum.

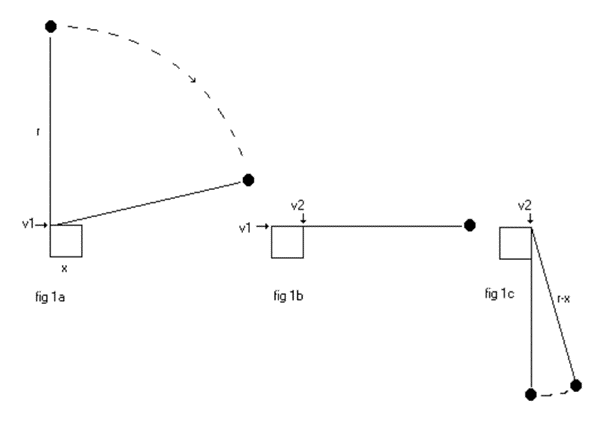
The unbalanced force. We consider a body, initially tracing a circular path, which then begins to move towards its spin axis². The example shown in fig 1, consists of two cylindrical masses joined by a light string.

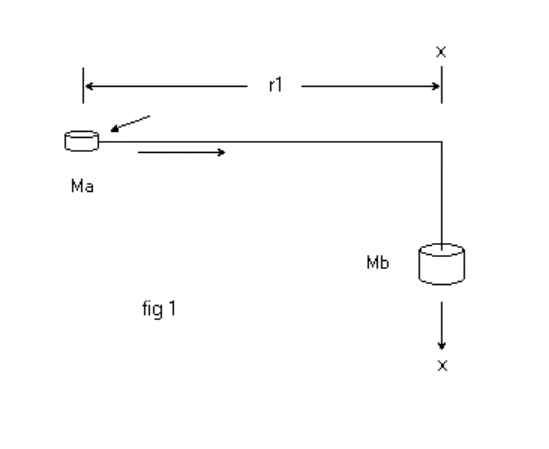
We can think of the mass Ma as a puck, sliding without friction on a horizontal surface. The string passes without friction through a hole in the surface at x-x. Ma orbits the rotation axis x–x at an initial distance r₁, and initially traces a circular path at an initial orbital (tangential) velocity v₁. The cylinder Mb is initially stationary. By suitable choices of masses and the initial angular velocity of the puck, the centrifugal force acting on the puck Ma can be made just less than the gravitational force acting on the cylinder Mb.

We seek to show that some of the “gravitational potential energy” lost by Mb as it falls, is transferred to the rotational kinetic energy of Ma.

Neither the radial centripetal force exerted by Mb on Ma, nor the centrifugal force experienced by Ma can affect the rotational kinetic energy of Ma since both act at right angles to the tangent to the circular locus of Ma. However, at the instant that the radius begins to shorten, the locus of the centre of mass of Ma begins to describe a spiral. Then, as depicted in fig 2a, the centrifugal force acting on Ma will be in the direction perpendicular to the tangent to the spiral³. (The radius of curvature is easily found using the tangential-polar equation⁴.) In fig 2a, Fc shows the direction of the actual centrifugal force, and Fn the direction of the component normal to the string joining Ma and Mb. It is this component of centrifugal force which acts to increase the rotational kinetic energy of the puck Ma.

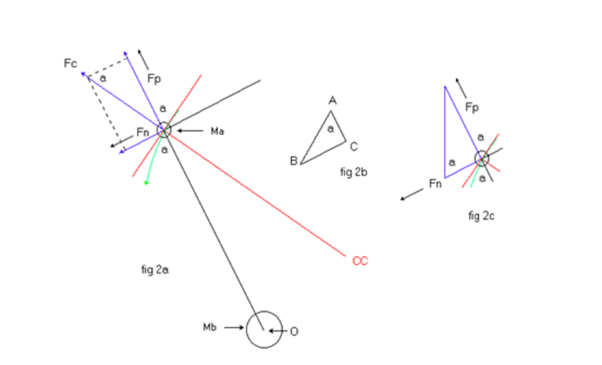
The centre of mass of Ma, describes a curved locus, shown in green, which spirals in towards the rotation axis (x-x in fig 1) which is into the page through O. Shown in red, are the tangent to the locus, the radius of curvature, and the instantaneous centre of curvature of the curved locus, cc (“instantaneous” because the centre of curvature moves continuously, as shown in figs 3a and 3b, which is the output of the Visual Basic program “IdealisedSkater”). The string is from O to Ma. The extension of the line beyond Ma (in blue, Fp) shows the direction of the radial component of centrifugal force.

In fig 2b, the actual distance travelled by the centre of mass of the puck along the spiral locus during the iteration period Dt is shown as the side AB of the displacement triangle ABC. The finite change in radius is the length AC. CB is the effective orbital displacement. AB and CB are of course curves. In the computer model we treat them as straight lines and acknowledge the slight inaccuracy thus produced. With an iteration time of 1m second, the calculation is correct (i.e. angular momentum is conserved) to twelve significant figures, or one part in a thousand billion. With shorter iteration periods the accuracy improves. In fig 3a, the locus of the centre of mass of Ma is shown in green and the locus of the centre of curvature of the spiral is in red. In fig 3b we zoom in on the locus of the centre of curvature.

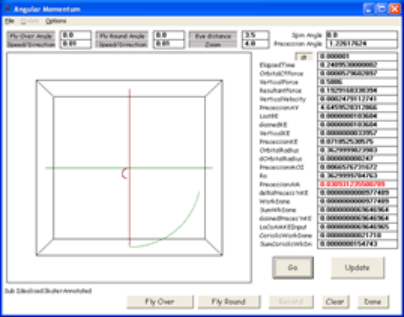
fig 3a

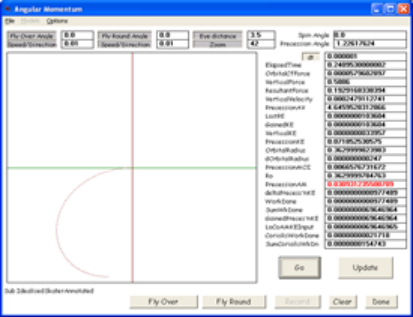
fig 3b

[ The Coriolis Force. It can be shown³ that the Coriolis force acts in the opposite sense – clockwise in the diagrams above – and would cause the puck to slow down, whereas in fact, like the ice skater pulling in her arms to execute a fast spin, the puck spins faster. For completeness the Coriolis force is dealt with in detail in the mathematical model.]

Having shown that centrifugal force is indeed capable of increasing the rotational kinetic energy of the puck – and the ice skater, we now wish to discover how Nature ensures that the energy thus transferred is exactly that required to conserve angular momentum.

The accelerating force must exist at the instant that the locus of the centre of mass of the puck changes from circular to spiral. Focussing our attention on that fact, we examine the energy input per meter (De/Dr) needed to conserve angular momentum as the puck moves from a distance r1 from O to a shorter distance r2. We note that as the difference between r1 and r2 is made smaller, De/Dr approaches a limit, the value of which is numerically equal to the instantaneous centrifugal force when r = r1.

Thus, in the limit, if de/dr = f, then de = fdr . (2)

This shows that at the instant that the locus of the centre of mass of the puck changes from circular to spiral, the (radially directed) centrifugal force, acting over an infinitesimal of distance, would supply exactly the energy needed to conserve angular momentum. This is an astonishing result. Our calculation of energy per meter (of radial displacement of any rotating mass) does not involve forces in any way (see fig 4). We are simply applying the ‘rule’ that angular momentum must be conserved. It is not at all obvious from our starting point, that we will arrive at the fundamental Newtonian energy equation.

The radially directed component of centrifugal force is of course in the wrong direction to increase rotational kinetic energy, but as shown in fig. 2, the force and displacement vector triangles (fig 2c and fig 2b respectively) are similar, having angle ‘a’ as a common angle, and thus the products of force and distance will be the same. Thus the product of the instantaneous orbital component of centrifugal force and the infinitesimal orbital displacement also provide the required energy, and in this case the force is in the right direction to increase the energy of the puck, and of course it is unbalanced.

That the calculated value of De/Dr approaches a limit, and that that limit is the centrifugal force, has considerable significance. It is thus that the deep underlying cause of the illusion of angular momentum conservation is revealed. Regardless of the mass of the rotating body and the inward force applied, at every point on the spiral, the instantaneous orbital component of centrifugal force, acting over an infinitesimal of distance, provides exactly the energy needed to conserve angular momentum in accordance with equations 1a and 1b. As is shown in a separate paper, in similar systems where no energy source is available, angular momentum is not conserved. (Treating the differential operator as though it were an ordinary number in (2) above is legitimate⁵ in this case since we are dealing with finite differences in the numerical program used to perform this analysis (see fig 4) and can therefore be confident that the result reflects the real physical situation..)

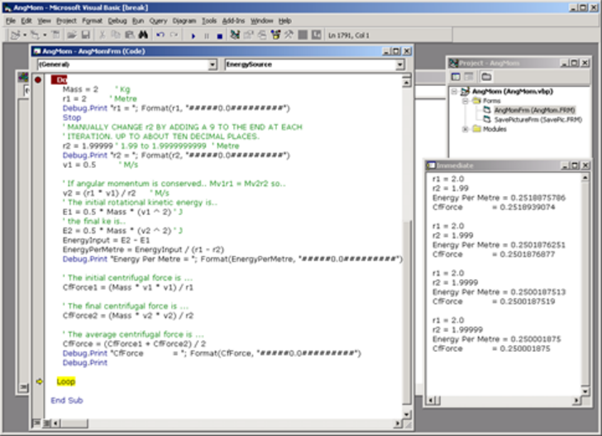
fig 4

To confirm the results experimentally, a mechanical device was constructed to simulate the spinning ice skater. This device conserves angular momentum to +0% and –2%. A first principles numerical model of that device again conserves angular momentum to twelve significant figures, and closely models the dynamical behaviour of the experimental device.

Numerical models

A first principles numerical model of an idealised ‘skater’ consisting of just the two masses shown in fig 1 was constructed. The model conserves angular momentum to better than twelve significant figures, and can be interrogated to check the actual forces at work.

Real Skater program

The real experiment and its numerical model will now be described. Initial conditions such as angular velocity are taken from the particular experiment run being modelled. Though essentially similar to the simple model above, the need to model all the moving parts naturally leads to greater complexity. The “RealSkater” program conserves angular momentum to 12 significant figures with an iteration time of 1ms. In modelling the fall of the arm from the horizontal to the point where the arm starts to rise again (1.1483 rads in this particular run) the first 12 significant figures are constant. Similarly, the sum of work done by the orbital component of centrifugal force is in near perfect agreement with the energy input required to conserve angular momentum. For example, at the point where the arm starts to rise again, to exactly conserve angular momentum there should have been an input of 0.0984158456960889 joules of energy. The model predicts that the sum of work done by the orbital component of centrifugal force (Fn) at that point will be 0.0984158456958144 joules.

The Skater Experiment The experiment shown in the photograph below (fig 5), simulates the spinning skater, pulling her arms to her sides to increase her angular velocity.

Fig 5

The “hands” are heavy metal spheres; the light but rigid “arms” are hinged at the “shoulder” so that they can rotate in the vertical plane. The bearings are very free. With the arms extended, the platform is set spinning. A fine thread supporting one arm is then broken. The mass starts to fall, and the platform’s angular velocity increases. Evenly spaced 1mm holes close to the edge of the circular platform allow light from an LED to fall onto a phototransistor. The pulses thus generated are timed, using a PC-based data recorder. As the mass begins to fall, a component of centrifugal force starts to oppose the torque due to gravity, about the hinge at the shoulder. As the spin rate increases, centrifugal force increases and as the mass falls further its effective component increases. Eventually the torque due to centrifugal force exceeds that due to gravity and the rotation about the hinge, in the vertical plane, starts to slow. When this rotation stops and reverses (the arm starts to rise), the force causing the platform’s angular acceleration also reverses and rotation about the vertical axis starts to slow. The shoulder “joint” is a low torque conductive plastic potentiometer, the output voltage of which varies as the arm rises and falls. A passive mixing network superimposes the pulses from the phototransistor onto this voltage. Charts 1 and 2 show a typical output.

Chart 1.

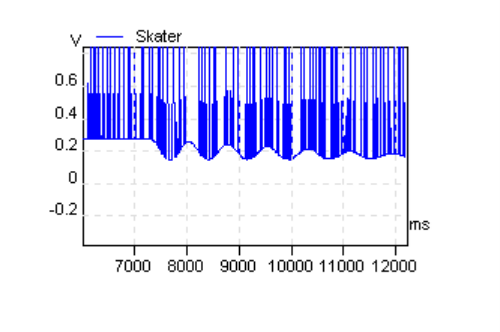
Chart 2 (detail from chart 1)

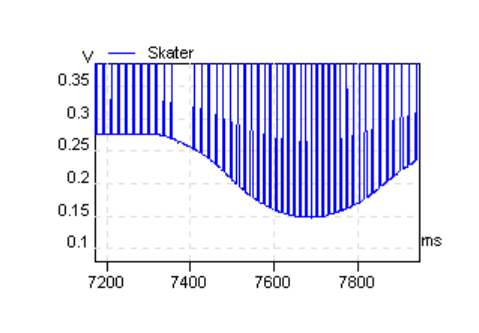
The point of reversal of the force can be seen in the recorded data at about 7.69 s in the example. At this point the mass has no kinetic energy in the vertical plane about the shoulder joint. The total kinetic energy of the system is then due only to rotation about the vertical axis. Angular momentum and rotational kinetic energy can thus be calculated along with energy loss due to friction.

Comparing the model with the experiment

The experiment shown in charts 1 and 2 lost about 1.02% angular momentum. This and other results are shown below.

-1.83001955566521% expt 3010_6

-1.79377498488112% expt 3010_8

-1.8988176472917% expt 3010_9

-1.0239011599485% expt 3010_11

-0.838896084187226% expt 3010_15

The measured starting values from each experiment are entered into the model and the model is re-run. The output is stored in a database. As well as agreeing that angular momentum is conserved to the degree shown above, the model’s prediction of the point of closest approach of the mass to the vertical axis and the time taken to reach that point are in excellent agreement with the measured values, as detailed below, clearly showing that the underlying physics is as described by the model.

The uncertainty in the measured value of Orbital Radius is .005 m. The uncertainty in the measured value of time is ± 0.0045 s.

Orbital Radius (m) Time to reach this point (sec)

ID Model Experiment Model Experiment

301006 0.26251074 0.265 0.362931 0.363

301008 0.26560865 0.267 0.363666 0.358

301009 0.21174287 0.222 0.408491 0.415

301010 0.24023572 0.245 0.384604 0.374

301011 0.24115455 0.250 0.384378 0.378

301015 0.19310891 0.21 0.41897 0.426

Conclusion.

The computer mathematical model provided here (“IdealisedSkater”), shows to any desired accuracy, that during any finite time period (Dt), the average value of the orbital component of centrifugal force, acting over the finite distance BC (fig. 2b), provides (or dissipates) the energy needed to conserve angular momentum in accordance with 1a and 1b above, as the centre of mass of the puck travels the radial distance AC. The accuracy of the model increases as Dt reduces. In the limit, angular momentum is exactly conserved in such systems because the instantaneous value of the orbital component of centrifugal force, acting over an infinitesimal of distance, provides or dissipates exactly the energy required to conserve angular momentum.

References.

This is the conventional view. In fact nothing happens to the mass of a body in free fall. The increase in mass due to acceleration being exactly cancelled by the decrease in mass due to the increase in the strength of the gravitational field.
Such a system is of course invariant under a Lorentz transformation. The ice skater is usually moving linearly at the moment that she begins to execute a fast spin, but angular momentum is still conserved, and the energy input is still as stated in 1a and 1b.
Meaningful Engineering Science, by S. H. Rutherford.
Advanced Mathematics, Geary, Lowry and Hayden
The Road to Reality, Penrose, page 493

An exception to the Law of Conservation of Angular Momentum

When the distribution of mass changes within an isolated spinning system, and angular momentum is conserved, an energy flow is always evident. An example is when a high diver jumps from a diving board, and curls up into a ball to decrease his moment of inertia and thus increase his spin rate. The diver will tell you that it takes effort to curl up; his muscles have to provide the energy required to conserve angular momentum. The question this paper addresses is – what happens as the distribution of mass changes, in systems where there is no available energy supply? The answer exposes another instance of Nature’s astonishing cleverness. The experiment presented here is not an isolated system. The measured loss of angular momentum is about 30%. The mathematical model predicts a loss of 30.4%. The model conserves energy to about ten significant digits. All that remains is to decide if it is reasonable to assert that the angular momentum lost by one part of the system is gained by the rest. Simple arguments of symmetry finally resolve the matter.

The Conservation Laws

Hermann Von Helmholtz first proposed the Law of Conservation of Energy in 1847, before all its forms had even been identified. All subsequent experiments have confirmed the soundness of his intuition; but we do not understand it.

Sometimes it is enough to know that it can be relied upon, but surely for most of us, blind faith is a poor substitute for understanding. But where energy is concerned, we have no choice; we know too little about the structure and properties of elementary particles and radiated energy. For example, we cannot begin to understand what happens to an electron falling in a gravitational field. We know from the work of Dirac that the electron occupies a finite volume of space, due to some internal vibratory motion – its Zitterbewegung – but we know almost nothing about the shape of this volume or the trajectory of the point charge within it. As the electron falls, gravitational potential energy is transformed into kinetic energy and mass. How that transformation takes place we do not know; what changes occur within the electron as a consequence, we cannot begin to guess.

Strangely, the origins of angular momentum conservation are far harder to trace. Examples of the phenomenon are cited in all college physics text-books – spinning skaters, tumbling high divers, toe dancers, men standing on rotating platforms with weights in their hands – all are said to conserve angular momentum as they change the configuration of their mass. But nowhere can we find any attempt to explain how angular momentum is conserved, except by analogy with linear momentum (which we will see is an astonishingly poor analogy). No elucidating mathematics is offered in such texts, and no famous names or experiments are ever mentioned. It seems the concept, once mooted, had its own unstoppable momentum, so that now, we do not even ask how angular momentum is conserved.

It is surely without precedent in science that the discovery of a fundamental physical law should go unclaimed? The reason is not hard to find. It is a trivial matter to show that angular momentum can be created or destroyed by converting angular momentum into linear momentum and vice versa. In free space, two identical masses are joined by a light string. First, imagine that each mass is a solid sphere. The common centre of mass of this two mass system has no translational motion relative to a standard inertial frame, but the masses are rotating about an axis (which we will call the orbital axis) through this common centre of mass. Each sphere has two components of angular momentum. The first is its orbital angular momentum about the common centre of mass. The second is angular momentum about its polar axis – its ‘intrinsic spin’ angular momentum. If we cut the string, each sphere moves off in a straight line. Each is still spinning about its polar axis with the same angular velocity, and thus still has the intrinsic spin component of angular momentum that it had before the string was cut, but its orbital component has been converted into linear momentum. Angular momentum has disappeared, and in its place we have a quantity of linear momentum. If we now start the experiment again but replace each sphere with a pair of spheres joined by a string as in fig 1, we can convert more angular momentum into linear momentum.

We can repeat this many, many times till we are left with two fundamental particles, and we know ¹ that they have no intrinsic spin angular momentum about an axis parallel to the original orbital axis. If we cut the imaginary string joining them we have lost all of the original angular momentum. In its place we have a quantity of linear momentum. If angular momentum had disappeared completely i.e., if it had not been converted to linear momentum, energy would have disappeared with it.

Going back to our initial experiment, let us say that M is the mass of each sphere, R its distance from the orbital axis, v the tangential velocity before the string was cut and the linear velocity after, and w the angular velocity before the string was cut. At the instant that the string is cut, the angular momentum is 2MvR (we can ignore the angular momentum due to intrinsic spin because it does not change in the transition), an instant later the linear momentum is 2Mv! How can we sensibly draw analogies between these two quite different measures of momentum? Only when we consider the energy before and after cutting the string can we make a connection between the two states. Before the string is cut the energy is ½Iw² = ½MR²w² (and, since v = Rw,) = ½MR² v²/R² which reduces to the linear form – ½Mv².

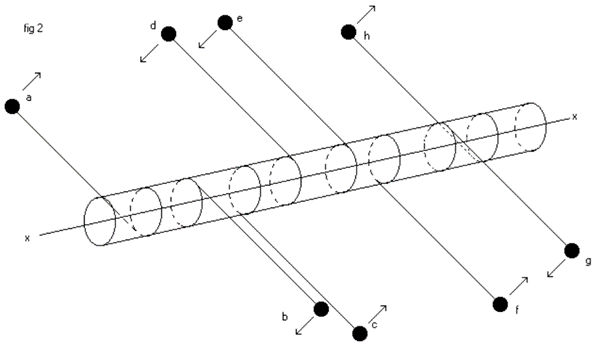
The Experiment A rigid bar of square cross section is attached horizontally to rigid and massive vertical side supports (fig 2). A small metal sphere is attached to the bar by a light steel wire. Two pairs of lasers and phototransistors feeding an a/d converter, supply a PC based data recorder. The first laser/phototransistor pair is positioned at the highest point of the sphere’s trajectory, and serves to measure the remaining kinetic energy of the sphere when it is at its point of maximum potential energy. The second pair measures the kinetic energy of the sphere when the wire has shortened by wrapping round the bar one complete turn. (The photograph is not of an actual experiment run, it is “posed”. The position of the mass when the photograph was taken was sheer good luck).

Fig 2

After an initial impulse the sphere falls under gravity to its lowest point. Its kinetic energy is then at its maximum value. There are energy losses due to friction and increasing tension in the wire, but no further energy gain. The average energy loss over a number of experimental runs is about 2 to 3 percent. The average reduction in angular momentum is about 30%; in good agreement with the prediction of the computer model (-30.4%). Some actual experimental results are shown below, more are available from the author’s web site. The code for the computer model (“WrappingSquareXS”) is also available from the author’s web site or as supplementary information from the publisher. For completeness, a second model (“WrappingCircularXS”) describes the more general case where the bar is a cylinder and gravity is absent. Both models work from first principles, employing only basic Newtonian mechanics.

WrappingSquareXS Experiment Results

Experiment ID Angular Momentum Loss (%) Energy (%)

3009_5 -29.4335231087941 -3.68455507701671

3009_6 -31.7598904788318 -1.91486253636183

0110_2 -30.4865058826114 -3.99647886907104

0110_4 -31.2916814901479 -1.78173721087519

0110_6 -29.1347202225657 -0.755400289708962

Note that angular momentum is not converted, it is lost. If it had not disappeared – if it had been conserved – then we could have applied the simple mathematics of angular momentum conservation to show that the energy of the system had increased. Since there is clearly no source of energy, we would have been forced to conclude that energy had somehow been created!

In fig 1a, the point of contact of the wire with the bar is the vertex v1, and clearly this is the spin axis. And since the mass orbits this axis for p/2 radians until it reaches the position shown in fig 1b, all the time tracing a circular arc, v1 is also the centre of curvature. The wire then shortens by the length of one side of the square bar, x, and the mass then orbits the vertex v2 for a further p/2 radian, tracing a circular arc of radius (r-x) as in fig 1c. Again there is no doubt that the instantaneous centre of curvature and the spin axis are coincident at v2. Since at all times, the spin axis and the centre of curvature of the locus of the mass are coincident, centrifugal force is always directed along the wire. So there is never a component of centrifugal force normal to the wire and therefore no accelerating force.

We can extend this reasoning to a bar of pentagonal or octagonal cross section. The point of contact of the wire with each vertex will still be both the centre of curvature of each of the five, or eight circular arcs, and the “momentary” spin axis. We can increase the number of sides until, in the limit, the cross section of the bar is effectively circular, the wire is tangent to the bar and the instantaneous point of contact of this tangent is both the instantaneous centre of curvature of the curve, and the instantaneous spin axis.

Nor can we invoke Coriolis acceleration. The Coriolis acceleration would be the sum of the components normal to the wire, of centripetal acceleration towards the instantaneous centre of curvature, and acceleration tangential to the locus of the centre of mass of the sphere. The centripetal acceleration clearly has no component tangential to the locus and so cannot accelerate the mass. There is a tangential acceleration but that is negative and due to the slowing of orbital or tangential speed required by the law of conservation of energy as the intrinsic spin energy of the sphere increases with increasing angular velocity (see End Note 1). There is thus no Coriolis acceleration to provide the means of transferring energy to conserve angular momentum, which is fortunate since there is no energy to transfer.

Note the elegance with which Nature avoids expending energy to displace the mass. The point of contact in figures 1a and 1b moves towards the mass – at no time does the mass move towards the point of contact.

As yet we have said nothing about the other part of the ‘system’ in our experiment.

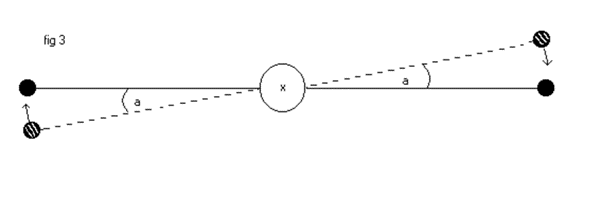
Since this is not an isolated system, we should consider the possibility that the earth gains the angular momentum lost by the mass. There is only one mechanism through which this could occur. The centrifugal force exerted by the mass applies a twist to the bar, dissipating energy as heat in the process. Perhaps the frame to which it is attached moves by some small amount – the effect may even reach the wall – or adjacent buildings, but at each point it will dissipate more energy as heat. Eventually, all of the available energy will be dissipated, and the earth will continue to rotate at its original angular velocity and with the same angular momentum, though it may well be slightly warmer. The energy lost by the experiments was easily measured and was found to vary between 0.8 j and 2.0 j. The experiment duration is less than two seconds. This represents an absolute maximum power of 2.0j / 2.0s = 1 watt. To assert that the earth could be moved by such a small effort would be absurd in the extreme, however, for the sake of completeness, the following thought experiment, which is the real experiment transformed into an isolated system, resolves the matter, using no more than arguments of symmetry. Eight identical masses are needed for a completely stable system, all rotating at the same angular velocity around a cylindrical bar in free space (fig 2).

The strings connecting the masses to the bar are light, thin and of equal length. The attachment of the strings to the bar is as shown by the solid lines in fig 3. The orbital planes of all the masses are normal to the x..x axis of the bar.

It’s best to think of the masses as pairs. In fig 2 the pair a-h and the pair b-g rotate in the same sense, and by symmetry produce no net forces or torques except the torque tending to turn the cylinder about its x..x axis. Let’s call this +L. To counter this torque, pairs c-f and d-e rotate in the opposite sense, and again by symmetry

produce no net forces or torques except the torque tending to turn the cylinder about its x..x axis in the opposite sense, -L. The cylinder is thus stable and stationary in space and does not rotate, and the strings attaching the masses to it are free to wrap round it, the system losing angular momentum, but conserving energy as they do so. Initially, in principle at least, the masses could be simultaneously set in motion by the release of compressed gas from a cavity in each mass. They would then accelerate through a small angle a, as in fig 3. During this initial acceleration period, energy would be transferred from the escaping gas

to the masses as kinetic energy, and to the strings as potential energy (the tension in the strings due to centrifugal force). From then on each mass would behave as described in the computer model provided (WrappingCircularXS).

End Notes.

1. What happens is this – if v is tangential speed, r the length of the string and w the angular velocity; with no accelerating force, initially v is unchanged as r shortens and w increases (since w = v/r). Since as yet there is no torque acting on the sphere, its intrinsic angular velocity lags behind w. A torque is thus generated because the line of the string, extended, no longer passes through the centre of mass of the sphere. Components of centrifugal force are then available to simultaneously increase the intrinsic spin rate of the sphere and reduce w. In the code we take the easy option and apply energy conservation.

Newtonian Particles and Spin

Composed January 1998. Amended April 2004, May 2005 and January 2011

Having shown how angular momentum is conserved in isolated spinning systems where the distribution of mass is changing¹, it is natural to ask if in fact angular momentum is always conserved. Is the conservation of angular momentum truly a fundamental physical law? The previous treatment removes the final instance of our dependence on the Law of Conservation of Angular Momentum but does not remove the law itself. Nor does it lead obviously to the conclusion that exceptions should exist.

Here we show that macroscopic (as distinct from quantum mechanical) angular momentum is not a property of material particles and therefore cannot be conserved for a single particle. Thus we show that if conservation of angular momentum is a fundamental law, then it can only apply to systems of more than one particle. By thus ‘diluting’ the law, we prepare the way for the discussion of exceptions.

Newton famously held² that material particles are point masses “incapable of rotation”. His reasoning is not known, but we can gain some insights into his thinking about spinning systems from The Principia.

He begins Book 1 with eight ‘Definitions’. These immediately precede his ‘Axioms, or Laws of Motion’. In the scholium to Definition VIII, the final paragraph contains a discussion of relative and absolute (true) motion. He was clearly aware of the absolute frame of reference provided by a rotating system. He says…

Also in the scholium following Proposition IV. Theorem IV, he provides an elegant definition of, and in fact ‘invents’, centrifugal force. Clearly Newton gave a great deal of thought to spin phenomena. In concluding that an individual particle could not rotate, it seems likely he reasoned along the following lines.

We begin by considering the difference in the way we calculate the rotational kinetic energy and angular momentum of macroscopic and microscopic bodies.

Essentially:

The equation describing a macroscopic body has two terms while the equation describing a microscopic particle has only one.

As an example of a macroscopic body, we consider a system similar to one of Newton’s “two globes”. A solid sphere of mass M and radius r, constrained to orbit some axis, which is stationary³ relative to a chosen reference frame. If the centre of mass of the sphere is a distance R (R>>r) from the axis and the orbital angular velocity is w, the total kinetic energy of the sphere is..

E_k = ½ MR²w² + ¹/₅ Mr²w² (1)

And its angular momentum is

H = MR² w + ²/₅ Mr²w (2)

If the constraint were to be removed (in Newton’s thought experiment, if the chord were to break), the first term on the right hand side of (1) would become the linear kinetic energy of the sphere, so we will refer to it as the linear term. The second term is the energy due to the intrinsic spin of the sphere, constrained or unconstrained, about the axis through its centre of mass, parallel to the orbital axis. Similarly, the second term in (2) would be the remaining angular momentum due to its intrinsic spin. It is worth noting that the first term in (2), MR² w, equal to MvR, would become Mv when the chord broke. Proof if it were needed that angular momentum and linear momentum are not interchangeable quantities.

We will take the electron as an example of a microscopic particle. Niels Bohr gave the value of the angular momentum of an electron orbiting a proton as..

H = MRv = MR²w

Note the absence of the intrinsic spin term that we have to specify in (1) for a macroscopic body in order to get agreement with experiment. Yet Bohr’s postulate is in agreement with experiment⁴.

This in itself shows that the electron has no angular momentum. But of course Newton knew nothing of this.

We now look more closely at the intrinsic spin component in (1)…

E_ki = ¹/₅ Mr²w² = ½ I w² (3)

where I is the moment of inertia of the sphere about its spin axis, which we will refer to as its polar moment of inertia. If we consider the sphere to be made up of a very large number of identical particles, each of mass m_p and distance r_p from the axis of spin, this can be written

E_ki = ½ S(m_pr_p²)w² (4)

which has the same form as the first term in (1), i.e. the linear term. This can also be written…

E_ki = ½ S(m_pv_p²) (5)

where v_p² = (r_pw)²

If we imagine the sphere breaking up into its constituent particles, each would travel linearly with kinetic energy…

E_kp = ½ m_pv_p² (6)

accounting between them for the available energy in (5).

Note: there is no energy left to attribute to the intrinsic spin of each individual particle.

Thus we see that material particles have no property equivalent to the polar moment of inertia of a uniform solid sphere about its axis of spin. If they rotate at all, in any sense, there can be no measurable kinetic energy associated with that rotation, or (1) would have a third term, and (3) a second. More importantly for the present discussion, without polar moment of inertia, a fundamental particle can have no intrinsic angular momentum, since, like rotational kinetic energy, angular momentum depends on the body, or particle, having a moment of inertia.

The introduction of electron spin by Dirac and Schrödinger (first suggested by Goudsmit and Uhlenbeck) has no effect on the above results. Our measurements of rotational kinetic energy are consistent. There is no contribution from quantum mechanical intrinsic spin.

Having justified Newton’s assertion, we ask… how can a point mass incapable of rotation, be bound by a law which sets limits on the behaviour of rotating systems?

Clearly, the angular momentum of everyday experience is a property of systems of more than one particle. If we speak of the angular momentum of individual particles, we are discussing a different phenomenon. The nature of quantum mechanical angular momentum is a mystery yet to be unveiled.

The work has relevance to the ongoing discussion relating to classical/quantum transitions, being one of the clearer examples of such a transition.

References:

2. Matter and Motion, by N Feather page 139, etc.

3. Not strictly necessary.

4. Bohr was of course treating the electron as a point mass. Hence the value Mvr. It was only later that Goudsmit and Uhlenbeck suggested that the electron had intrinsic spin (Atomic Spectra and Atomic Structure, by Gerhard Herzberg p. 93) and later still that Dirac and Schrodinger showed that the electron had spatial extension – its zitterbewegung or trembling motion which increases the speed of the point charge to the speed of light. (Relativistic Quantum Mechanics, by Paul Strange p. 210)

The Ferris wheel thought experiment

The law of conservation of energy asserts that energy can neither be created nor destroyed. When we see energy increasing in one part of an isolated system, we assume that it is being transferred from another part of the system, and often being converted along the way from one form of energy to another. For example, when a motor car accelerates, we know that chemical energy from its fuel is being converted first into heat and then into energy of motion. Also, when we carry an object up a flight of stairs to the top of a building, we know that its mass increases as it rises and we confidently assume that this increase in mass/energy is being provided by our muscles.

Here we describe a system, an idealised Ferris wheel, in which energy is both created and destroyed, and we show that the notion of transfer of energy from one part of a system to another is an illusion. Our (ten metre diameter) Ferris wheel (fig 1) has pairs of diametrically opposite carriages. All the carriages have exactly the same mass. We treat each carriage as a point mass on the rim of the wheel. The central bearing of the wheel is friction free and there is no air resistance. The spokes of the wheel are rigid and, like the rim, have no mass. The bottom of the wheel just skims the surface of the earth. The wheel rotates very slowly anticlockwise.

Fig 1

We know with the certainty that 100 years of relativity imparts that as the carriage at six o’clock rises to 3 o’clock and then 12 o’clock, its mass increases. Similarly, the 12 o’clock particle loses mass as it descends to the bottom of the wheel. We know that the mass gained by one carriage must be the same as that lost by the other, and our intuition is that energy is continuously transferred from the falling to the rising particle. But how? We can simplify the thought experiment further by removing the rim (fig 2), so that the carriages are only connected to each other by the spokes.

Fig 2

Even if we relax the “rigid” criterion and allow the spokes to flex, so that energy might be transferred somehow, we run into the problem that as they flex, the spokes generate heat and the system loses energy by radiation.

We could actually build such a device and put it in orbit around the earth. How astonishing it would be to see the rotation slow down as it lost energy by radiation: Nonsense of course.

There is no way that the energy lost by one carriage can be transferred to another. The energy of each carriage is determined solely by its height in the gravitational field. Each carriage gains mass as it rises and loses it again as it falls. Energy is only conserved statistically. Each individual carriage gains and loses mass with no concern whatsoever for our cherished principles.

The mass of each carriage at infinity, i.e., far from gravitational fields, we set at unity. The carriage at the bottom of the wheel (6 o’clock) therefore has a mass of 0.9999999993038747266344053675 kg, the carriages at 3 o’clock and 9 o’clock 0.9999999993038752729556592989 kg and the 12 o’clock carriage’s mass is 0.9999999993038758192760557217 kg.

We calculate these mass changes using the redshift equation, m1 = m0 * (1-(G*M/R*C²)). This relies on the gravitational constant G and the mass of the earth M, neither of which is known very accurately. Things are only improved slightly if we use the Standard Gravitational Parameter (SGP) – the product of G and M – which is known more accurately than each factor independently. We can check the validity of using the redshift equation by using e = mgh, but we have to play with the value of g to get the results to agree reasonably well. For example, if the carriages have a mass of 1kg at infinity, the difference in energy between the 6 o’clock carriage and the 12 o’clock carriage is…

98.20173417593804262272868081 J (redshift equation) and…

98.20173493163929037814931778 J (e = mgh) but to get this level of agreement we have to make the acceleration due to gravity at the surface of the earth equal to 9.8201735; which is bit high. (SGP = 398600441800000 kgm³ s^-2)

These difficulties, caused by our poor knowledge of the constants involved, make no difference to the fundamental principles being examined.

Conclusion

Energy is only conserved in the statistical sense that wherever a particle gains mass, another particle in the same isolated system loses the same amount of mass. The idea that energy is transferred from one part of a system to another is an illusion. (Recently read that Schrodinger had said this.)

Why light warps space 040720_1

The electron has a magnetic field due to the fact that it is a spinning charge. As it orbits the atom’s nucleus, its (intrinsic) magnetic field interacts with the (general) magnetic field of the atom; it’s called the “spin/orbit coupling”. This causes the spin axis of the electron to “wobble” backwards and forwards as it rotates. This motion is called the Larmor Precession.

When the electron emits light, the light moves outward from the electron as an expanding sphere; like a quickly inflating balloon. But the balloon is still precessing as if it were still part of the electron. The “balloon” of light is executing Larmor Precession.

The energy contained in any kind of wave motion is proportional to the wave’s amplitude and its frequency E_wa Af. In quantum theory the energy of a light photon is E = hf, h being Planck’s constant. So, h looks like the amplitude of the wave.

So as the light sphere expands, every point on its surface rotates with a constant amplitude h.

If the surface of the sphere is travelling outwards at the speed of light (which it is), how fast is any point on the surface travelling if it is also rotating?

Let’s say the bubble expands outward by some distance. Any point on its surface has to travel a greater distance in the same time. Which means it must travel faster!! But the bubble is already travelling at the speed of light, so any point on its surface would be travelling faster than light. This cannot happen so the light warps space along its track so as to keep the speed of light constant.

Why precession AV is substantially constant as the rotor is retracted.

Mechanical negative feedback As the rotor is retracted towards the precession axis, its precession AV must tend to increase due to the skater affect. However, any such acceleration must increase the gyro generated torque, causing the gyro to rise and generate an opposing torque. This negative feedback effect keeps the precession rate essentially constant as the gyro is retracted.

Leave a Reply Cancel reply