Antigravity

Survival

Stephen Hawking believed that if we are to survive, we must become a spacefaring species.

Elon Musk agrees, but even his state-of-the-art rocket technology can only get about 4% of launch weight to low earth orbit. Presently that equates to about six or seven people and all they need to survive for a few months. Clearly to get thousands of us into space, with supplies for years, a new technology is needed.

A strike by a rogue asteroid, or nuclear war, are real but unlikely species killers, but a more pressing threat to our survival is climate change. We are already seeing the consequences. Eventually, crops will fail, water supplies will fail… We have to stop using fossil fuels.

As renewable energy sources and battery technologies advance, we will be able to transition to “flying cars” and whatever aircraft evolve into. But we need an engine technology that runs on electricity. We believe that the Inertial Engine described here is that technology.

Antigravity

The Inertial Engine exploits two remarkable discoveries.

The first discovery was made when we built the device shown below (fig 1). It is easy to show mathematically and logically that the wheel of the offset gyroscope in fig 1 is weightless (see the ‘Gravity’ page fig 4 and fig 5 for details). In fact, because some parts of it are not weightless (axle, bearing etc), the wheel has to generate a small upward force – an antigravity force – in order to hold them up.

The device in fig 1 was actually built to measure the centrifugal force generated by this gyro configuration when it precesses. We show below that this gyro configuration cannot exhibit any centrifugal force (in the direction j to i in fig 3). Fig 4 is the output of the mathematical model that proves this (see the boxes labelled ‘Upper half centrifugal force’ and ‘Lower half centrifugal force’), and fig 5 shows the simple logic.

Fig 1

We can begin to describe the second discovery with the help of fig 2. We built the machine shown in fig 2 in 2006 to test some ideas we had for producing a lifting force. With this machine we could set the gyro wheel precessing steadily (i.e., without nutation) and then pull the rotor towards the vertical precession axis. Theoretical work and experiments with a small handheld device had suggested that the center of mass of the gyro wheel would rise as it was retracted, causing the wheel and its axle to rotate about the horizontal axis (a – b in fig 3).

Fig 2

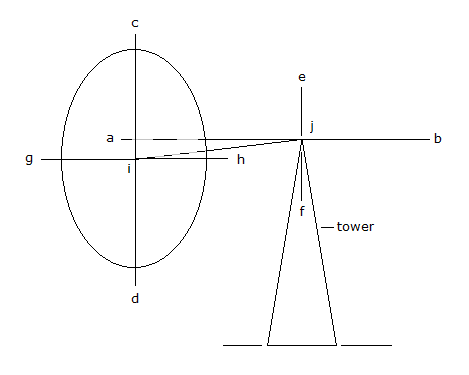
Fig 3

We had shown that the rotations (precessions) about the vertical and horizontal axes (e – f and a – b in fig 3) formed a mechanical negative feedback loop that would keep the precession (ω) about the vertical axis substantially constant as the gyro wheel was retracted. (See papers page ‘Why precession AV is substantially constant as the rotor is retracted’.)

As the orbital radius is thus reduced, if precession rate ω is constant, the tangential velocity of the gyro’s center of mass, and thus its kinetic energy, must reduce. Energy can’t just disappear, so the lost kinetic energy must be replaced with a gain in potential energy. Simple energy calculations showed that, to conserve energy, the center of mass of the wheel should rise a little less than one mm when retracted as far as possible, if we were pulling against centrifugal force.

The machine had four high precision shaft encoders and sophisticated electronics connected wirelessly to a computer running control and data storage software.

Two of the shaft encoders and their associated DC electric motors were jointly responsible for keeping the rotor spinning at a constant speed (Ω) and at the same time pulling the rotor towards the vertical precession axis. The mechanical design allowed these motors to spin at any speed necessary to achieve these two interacting functions.

The device provided no means of directly measuring the energy consumed by these motors, or the pulling force they were exerting. Because the device was rotating, we had little feedback other than the sound of the drive motors. We had already shown that this gyro configuration cannot exhibit any net centrifugal force (figs 4 and 5), implying that we would encounter very little resistance when we tried to pull the rotor towards the vertical precession axis.

Fig 4

Fig 5

What we actually found was that when we issued the command to retract the rotor at a constant rate, the two motors powering the retraction could be heard to be working extremely hard. Also the gyro wheel lifted very quickly and banged against the end stops, raising the center of mass of the wheel over 20 mm. Clearly the motors were having to generate a force many tens of times greater than would be expected if they were pulling against normal centrifugal force.

In the following months we tried very hard to explain these extreme results; including producing a mathematical model to take account of the fact that the gyro wheel follows a spiral path as it is retracted and taking careful account of the effects of friction. To this latter end we applied a trickle current to a motor connected to the vertical precession axle. By driving this axle we were able to estimate the energy lost due to friction.

We could find nothing within the known laws of physics to explain the resistance the motors were encountering. We finally concluded that we had stumbled upon something new, and eventually were able to show that the gyro was interacting with the background Inertial Field.

The theory of the Inertial Field

Many scientists, including Nordstrom, Kaluza, Rosen and Gödel, have at different times and for different reasons, proposed the existence of a universal background scalar field. Gödel called it an “inertial field”. More recently Higgs and others proposed, as part of the standard model, that such a field is responsible for giving material particles their (inertial) mass. It is now called the Higgs Field, and the quantum of the field, the so called Higgs Boson, may have been detected at CERN. However, despite its undoubted success, the Higgs Mechanism is not well defined.

Beginning in 1983, we approached the questions of particle mass and particle inertia by first developing a particle “design” that separates particle charge and particle gravitational mass (see the “Particles” section below), and treats particle inertia as a separate phenomenon. From 2006 we began to think of inertia as being caused by the interaction of the particle with a background inertial field.

Justification

There is a magnetic force and a magnetic field, an electric force and an electric field, a gravitational force and a gravitational field. There is also an inertia force – the resistance you feel when you try to accelerate a loaded shopping trolley – but no inertial field.

Arguments of symmetry suggest that there should be such a field.

Properties of the field

If we assume that the inertial field has the opposite effect to gravity on the speed of light, then our fermion theory explains inertia in a logically consistent way (see Inertia page). (The slowing of light by stronger gravity is equivalent to increasing the length of measuring rods and slowing down clocks. So the inertial field shortens measuring rods and speeds up clocks.)

It also explains the dark matter halos around galaxies…

As described by the theory of radial free fall, a gravitational field increases the de Broglie wavelength of a particle and thus reduces its mass. The inertial field does the opposite. Though the inertial field is a scalar field, its strength effectively increases as the strength of the gravitational field with which it coexists, reduces.

Close to a body like the earth, the effect of the inertial field is much less than the effect of the local gravitational field. But as we move out towards the edges of the galaxy, gravity gets weaker, and at some point, its effects are exactly equal and opposite to the effects of the inertial field. We refer to this as the “transition shell” where gravity still causes a small increase in the wavelength of a particle but the inertial field decreases its wavelength by the same amount.

At the transition shell the mass reducing effect of the galaxy’s gravitational field is exactly cancelled by the mass increasing effect of the inertial field and the particle thus has zero acceleration due to gravity i.e. – it is gravitationally buoyant.

During the quasar stage of the evolution of a galaxy, huge quantities of fermionic matter are thrown radially outwards away from the central black hole. The ADG of the particles thrown out by the quasar of course reduces as they move outwards towards the edges of the galaxy. Were it not for the inertial field, they would always have some finite ADG and would eventually stop rising and fall back into the galaxy (unless they started with the escape velocity for that galaxy). The inertial field changes that. At the transition shell, their ADG falls to zero. The particles have become gravitationally buoyant and are no longer attracted back into the galaxy. Galaxies should thus be surrounded by a cloud of matter that is not attracted gravitationally towards the galaxy. The particles in this cloud are attracted gravitationally to each other, but the effect of the inertial field swamps this attraction. Thus, stars will not form from this matter. These “dark matter halos” around galaxies and galaxy clusters have of course been observed and are presently the focus of much attention.

We are sure that the inertial field was responsible for the unusual experimental results we obtained in 2006. We explain in detail below.

The talk of kinetic energy and potential energy above is of course naïve. All changes in energy are actually changes in mass. If we lift a body at constant speed, the energy we expend increases the mass of the body, not its “potential energy”. If we apply a force to accelerate a body, we are actually increasing its mass, not its “kinetic energy”. However we do work on a body, we increase or decrease its mass.

Thus the force we apply to retract the rotor of the device in Fig 2, acting over a distance, increases the mass of the gyro wheel. Since it is not speeding up, it can only exhibit that increase in mass by rising in the gravitational field. The fact that we are working against the inertial field rather than centrifugal force is a bonus. We can input much more energy than we originally expected, and thus achieve much greater lift.

In 2012 when we felt confident that we had a sound theory of the inertial field, we performed a new experiment with a simple “wheel on a stick” gyro weighing 4 kilograms. We wanted to show that the wheel was rising because its mass was increasing and not because the gyro generated torque was turning it. This was a hand held device and it was possible to keep the axle (the “stick”) horizontal as the gyro lifted.

The experiment is very repeatable and anyone can perform it once they learn the knack. Just pulling in line with the stick doesn’t work. The vertical axis around which the wheel is precessing has to get nearer to the wheel – the stick has to shorten. It sounds more complicated than it is.

By measuring how high the wheel lifts, the energy input can be calculated approximately and from that and the distance through which we pull it, we can estimate the force we are having to apply.

It turns out that we are pulling against a force many tens of times greater than centrifugal force.

Thus, the second discovery was the interaction of the precessing offset gyro with the inertial field.

Particles

Before we can explain antigravity, we need to explain gravity, and in particular, why things fall. For that, we need a model of fermions that tells us how material particles interact with the gravitational field.

If you think gravity is already well understood you should watch Professor Jim Al-Khalili’s excellent video, “Gravity and Me”, on YouTube. At about 1:27:30 he talks about not knowing why things fall. He and Kip Thorn speculate what gravity might be, but it’s clear that there is no sound theory behind their guesses. Kip Thorne co-wrote the tome, “Gravitation”, with C W Misner and J A Wheeler. If those people don’t know why things fall, then nobody does.

The book, “What is the Electron” (V. Simulik 2005) describes seventeen models of the electron. Not one of these even attempts to explain how particles are affected by the presence of a gravitational field – and none of them attempts to explain why things fall.

The fermion model we now describe enables us to understand what gravity really is and why things fall when we drop them. This is our electron.

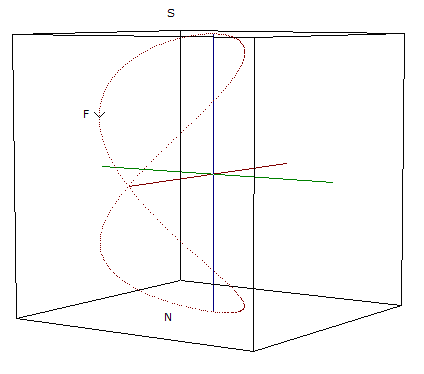
Fig 6

The arrow represents the electron’s point charge, which is a dimensionless, massless, point of light, rotating simultaneously around two perpendicular axes (red and blue in the drawing), thus tracing out the Lissajous figure-of-eight shown in the drawing. To get back to its starting point, the point of light must rotate through 2 X 360 degrees. Which explains why the electron has twice the classically expected magnetic moment. The gravitational mass and gravitational field of the electron arise because the three-dimensional Lissajous figure-of-eight track that the point of light describes is warped space – warped in the sense that an observer travelling with the point of light will measure the distance from N to S to be the same as would be measured along the vertical (blue) axis by a distant observer. (A full explanation of how and why light warps space is providedon the “Papers” page.) The electron’s wavelength (de Broglie wavelength) is the distance from N to S. The strength of the warp along the track is inversely proportional to the particle’s wavelength. The ‘clock rate’ is the time it takes for the point of light to make one complete circuit of 720 degrees. (This is discussed in detail In the section headed “The Electron Clock”.)

A key point to note… the speed of light is constant only in a constant gravitational field. For example, it has been shown (Shapiro et al) that light slows down as it passes close to the sun.

Theory of radial freefall

First we imagine creating an electron from light of energy 0.511 MeV, out in space, away from gravitational fields. The warp seen by the point charge (point of light) is just the warp along the electron’s own Lissajous figure of eight track – and nothing happens – the particle does not move. Now we imagine creating the electron close to the surface of the earth. The warp seen by the point charge is now the sum of the electron’s intrinsic warp and the warp of the external field. This increased warp would cause the point of light to slow down, so the electron immediately increases its wavelength to reduce the warp along the track, keeping the total warp constant. This increase in wavelength is a reduction of the electron’s mass/energy. Energy can’t just disappear, so the particle has to accelerate in order to maintain its original mass/energy. So now you know why things fall.

You may be wondering why the particle doesn’t accelerate sideways. We explain shortly why it falls downward (see fig 9 below).

Of course it is also true that if we lift a particle (at constant slow speed) in the gravitational field of the earth, its mass must increase (its wavelength must reduce) so that the warp along the track increases to compensate for the reduction in the warp of the external field. That way the point of light always sees the same warp and therefore always travels at the same speed – hence c for any given particle is a constant. Which it must be because if M and c were both able to vary, E = Mc² would not be a predictable quantity. The figure below is a view of the electron from N toward S and shows the constant amplitude of the electron wave. Our research (not shown here) suggests that this may point to the origin of Plank’s Constant.

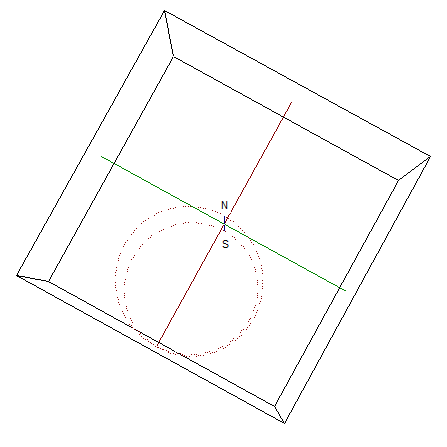
Fig 7

The figure below is a down quark (charge = – 1/3 e).

Fig 8

The Electron Clock

In 1924, Louis de Broglie’s suggested that the electron has an internal clock and that time dilation effects are effects on that clock. Experiments conducted by a French team between 2005 and 2010 confirmed de Broglie’s conjecture. See…

“A Search for the de Broglie Particle Internal Clock by Means of Electron Channeling”, M. Gouanère et. al., Foundations of Physics 38: 659-664. 2008

“Electron time, mass and zitter” David Hestenes, Arizona State University

“Reading the Electron Clock” David Hestenes, arXiv:0802.3227v1, 21 Feb 2008

Particle clock rate allows us to understand how nature distinguishes between an increase in mass due to increased velocity and an identical increase in mass due to increased height in the gravitational field. If nature were unable to distinguish between the two, Newton’s laws would not exist, and the universe would be chaos. We explain this in greater detail in our paper, “The Mass, Clock-rate Principle” (MCP).

The “L Matrix of Particle Mass and Clock-rate” below helps understanding.

In the diagram, changes in mass are indicated by changes in size, and changing clock rate by the changing position of the clock “hand”. For example, if the particle’s mass increases and its clock rate decreases, the particle’s velocity has increased (row 9). If the particle’s mass increases and its clock rate also increases, the particle’s height in the gravitational field has increased (column A). It’s very important to realise that the converse is true; if for any reason a particle moves to a particular cell in the matrix, it must have the mass and clock rate associated with that cell. This is explained in detail in the Mass Clock-rate Principle paper.

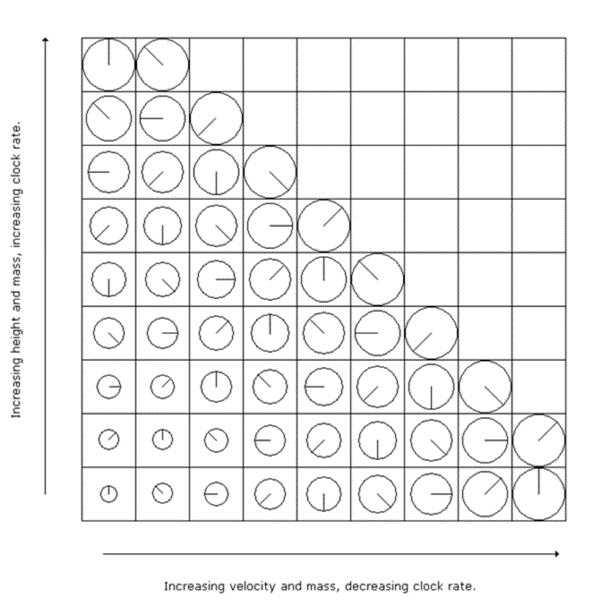
Fig 9

We are now in a position to explain why an object accelerates downwards when we release it rather than sideways.

In the L Matrix above, we imagine that the particle is created at 1A. As explained above, its mass is reduced by the field, so the only place it might exist is at 2A, (or 3A or maybe 4A depending on how much mass it has lost). So that’s where it moves to, i.e. downward.

This loss of mass violates energy conservation, so the particle accelerates to 2B (or 3C etc.) to keep its mass constant. But by now it is in stronger gravity, which again reduces its mass, so it has to fall and then accelerate again. Close to the surface of the Earth a constant acceleration of a little over 9.8 m/s/s keeps the mass of the particle constant.

The mass loss due to gravity must occur before there can be a mass gain due to velocity. The uncertainty principle allows the momentary violation of energy conservation that this requires and sets a limit on the delay between mass loss and mass gain. (Some dispute the validity of the energy/time uncertainty principle. We refer the reader to the 1930 Solvay conference in Brussels where Einstein and Bohr debated the matter at length.)

Certainly, in order to make any progress with quantifying radial free fall (i.e. freefall towards the centre of the Earth), it is necessary to treat this as a two-step process, and accept that the second step – an increase in velocity, cannot happen without the first step – a loss of mass due to the particle’s interaction with the gravitational field.

So the particle zigzags (in the L matrix, not in space) from A1 to A2, then B2, then B3 then C3 and so on. Note that the clock rate slows because it is accelerating and slows further because it is moving into stronger gravity. Thus, though its mass is essentially constant, Nature knows that the particle is moving because its clock rate is slowing and knows that it is falling because its clock rate is slowing twice as quickly as if it were just accelerating. Now that we know what gravity is and why things fall, we can get on with explaining why a body might rise in a gravitational field. Fortunately, the offset gyroscope provides us with an actual example, so we first need to understand how gyros really work.